图

2018-02-20

图的表示

邻接矩阵

n*n的矩阵，有边是1，无边是0

a, b, c, d, e, f, g, h = range(8)
N =[
  [0, 1, 1, 1, 1, 1, 0, 0],
  [0, 0, 1, 0, 1, 0, 0, 0],
  [0, 0, 0, 1, 0, 0, 0, 0],
  [0, 0, 0, 0, 1, 0, 0, 0],
  [0, 0, 0, 0, 0, 1, 0, 0],
  [0, 0, 1, 0, 0, 0, 1, 1],
  [0, 0, 0, 0, 0, 1, 0, 1],
  [0, 0, 0, 0, 0, 1, 1, 0],
]

关于邻接矩阵：

主对角线为自己到自己，为0
行和为出度
列和为入度

邻接表

为每个点建立一个链表（数组）存放与之连接点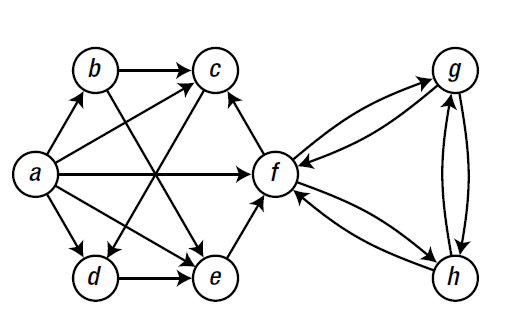
upload successful

a, b, c, d, e, f, g, h = range(8)
N = [
  {b, c, d, e, f},
  {c, e},
  {d},
  {e},
  {f},
  {c, g, h},
  {f, h},
  {f, g}
]
# N(v) 代表的是 v 的邻居节点集；

>>> b in N[a]         # neighborhood membership
True
>>> len(N[f])         # out-degree：出度
3

加权邻接表

使用 dict 类型来代替 set 或 list 来表示邻接集。在 dict 类型中，每个邻居节点都会有一个键和一个额外的值，用于表示与其邻居节点（或出边）之间的关联性，如边的权重。

a, b, c, d, e, f, g, h = range(8)
N = [
  {b:2, c:1, d:3, e:9, f:4},
  {c:4, e:4},
  {d:8},
  {e:7},
  {f:5},
  {c:2, g:2, h:2},
  {f:1, h:6},
  {f:9, g:8}
]

>>> b in N[a]         # neighborhood membership
True
>>> len(N[f])         # out-degree
3
>>> N[a][b]          # Edge weight for (a, b)
2

图的实现

有下面一张图：

A -> B
A -> C
B -> C
B -> D
C -> D
D -> C
E -> F
F -> C

可以用字典和列表来构建
graph = {'A': ['B', 'C'],'B': ['C', 'D'],'C': ['D'],'D': ['C'],'E': ['F'],'F': ['C']}

找到一条路径

def find_path(graph, start, end, path=[]):
        path = path + [start]
        if start == end:
            return path
        if not start in graph:
            return None
        for node in graph[start]:
            if node not in path:
                newpath = find_path(graph, node, end, path)
                if newpath: return newpath
        return None

找到所有路径

def find_all_paths(graph, start, end, path=[]):
        path = path + [start]
        if start == end:
            return [path]
        if not start in graph:
            return []
        paths = []
        for node in graph[start]:
            if node not in path:
                newpaths = find_all_paths(graph, node, end, path)
                for newpath in newpaths:
                    paths.append(newpath)
        return paths

找到最短路径

def find_shortest_path(graph, start, end, path=[]):
        path = path + [start]
        if start == end:
            return path
        if not start in graph:
            return None
        shortest = None
        for node in graph[start]:
            if node not in path:
                newpath = find_shortest_path(graph, node, end, path)
                if newpath:
                    if not shortest or len(newpath) < len(shortest):
                        shortest = newpath
        return shortest

图的搜索

广度优先搜索

BFS算法框架
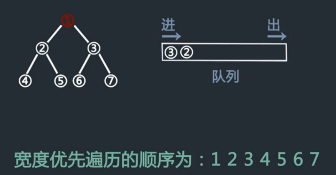
广（宽）度优先搜索（Breadth-First-Search）过程：

给定起点a，将a放入缓冲区，开始搜索
假定某时刻缓冲区结点为abc，则访问结点a的邻接点a1a2a3，同时缓冲区变为bca1a2a3
- 需要队列做辅助，先进先出

注意：

结点判重：判断是否已经访问过之前的节点
路径记录：一个结点可能扩展出多个结点，但最多只能有1个前驱（除了起始点），用到和节点数目等长的数组pre记录结点前驱pre[i]=j

upload successful

深度优先搜索

DFS算法框架
深度优先搜索（Depth-First-Search）
可以用栈的方法实现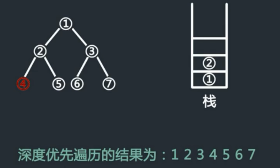
upload successful

深度优先搜索可以解决很多问题，比如八皇后、数独、LCA问题（Tarjan算法）

class Graph(object):

    def __init__(self,*args,**kwargs):
        self.node_neighbors = {}
        self.visited = {}

    def add_nodes(self,nodelist):

        for node in nodelist:
            self.add_node(node)

    def add_node(self,node):
        if not node in self.nodes():
            self.node_neighbors[node] = []

    def add_edge(self,edge):
        u,v = edge
        if(v not in self.node_neighbors[u]) and ( u not in self.node_neighbors[v]):
            self.node_neighbors[u].append(v)

            if(u!=v):
                self.node_neighbors[v].append(u)

    def nodes(self):
        return self.node_neighbors.keys()

    def depth_first_search(self,root=None):
        order = []
        def dfs(node):
            self.visited[node] = True
            order.append(node)
            for n in self.node_neighbors[node]:
                if not n in self.visited:
                    dfs(n)
        if root:
            dfs(root)

        for node in self.nodes():
            if not node in self.visited:
                dfs(node)

        print (order)
        return order

    def breadth_first_search(self,root=None):
        queue = []
        order = []
        def bfs():
            while len(queue)> 0:
                node  = queue.pop(0)

                self.visited[node] = True
                for n in self.node_neighbors[node]:
                    if (not n in self.visited) and (not n in queue):
                        queue.append(n)
                        order.append(n)
        if root:
            queue.append(root)
            order.append(root)
            bfs()

        for node in self.nodes():
            if not node in self.visited:
                queue.append(node)
                order.append(node)
                bfs()
        print (order)

        return order
g = Graph()
g.add_nodes([i+1 for i in range(8)])
g.add_edge((1, 2))
g.add_edge((1, 3))
g.add_edge((2, 4))
g.add_edge((2, 5))
g.add_edge((4, 8))
g.add_edge((5, 8))
g.add_edge((3, 6))
g.add_edge((3, 7))
g.add_edge((6, 7))
print ("nodes:", g.nodes())

order = g.breadth_first_search(1)
order = g.depth_first_search(1)

最短路径

Dijkstra算法

是一种贪心算法，求出某点到所有点的最短路径，这样问题就解决。可以解决带权最短路径的问题，权值不能为负值。
优化：启发式A*算法、GIS

Floyd算法

又叫做插点法，用于寻找给定过的加权图中多源点之间最短路径算法。Floyd算法的权值是可以为负值的。

Bellman-ford算法

适用于单源节点到其他所有节点的最短路径。

最小生成树

Prim算法

以一个节点作为最小生成树的初始节点，然后以迭代的方式找出与最小生成树中各节点权重最小的边，加入到最小生成树汇总。如果加入后缠身回路，则跳过这条边，选择下一个节点。最终将所有节点都加入到生成树停止。小树–>大数

Kruskal算法

与Prim不同，Kruskal算法在找最小生成树结点前，对所有有权重边从小到大排序，将排序好的权重依次加入到最小生成树种，如果加入产生回路则跳过。最终将所有节点都加入到生成树停止。森林–>大树

为了加快判断候选边e的加入是否形成环，可以考虑用并查集的方法：把当前状态的每个连通子图保存在各自的集合中，候选边是否可以加入，转化成两个顶点是否位于同一集合中。

Kruskal算法可以解决MST问题。

拓扑排序

对一个有向无环图（Directed Acyclic Graph）G进行拓扑排序，将G中所有顶点排成线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在现行排序中出现在v之前。
相互关系不变形。拓扑排序是一种偏序的。