人工智能——决策树算法

决策树

决策树（decision tree）是什么?要想解决这个问题，首先要弄明白的就是计算机中的树是什么。树，我们在计算机中很常见了，有二叉树，哈夫曼树等等，总结一下共同点的时候就是，对一个当前节点而言，下一个个节点有多个节点可以选择的结构。简单的说就是有分叉的结构就是树（可能这样说也不严谨）。而决策树就是利用了这种分叉来判断的树。
决策树以树状结构表示数据分类结果。包含

• 一个根节点
• 若干个非叶子节点（决策点、测试条件）
• 若干个叶子结点（分类后所得的分类标记）
• 分支（测试结果）
  

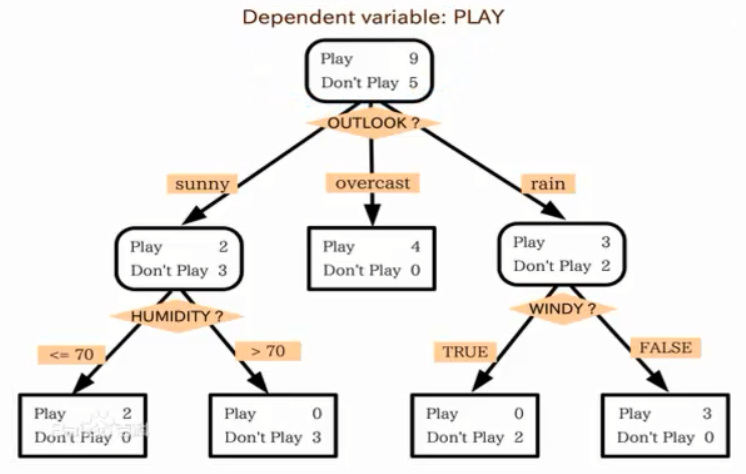
信息论

熵的概念

几个重要的概念：

• 由$P(X,Y)=P(X)*P(Y)$事件X和Y相互独立的特性，可以得知：$$\log_{}(XY)=\log_{}(X)+\log_{}(Y)$$
• $H(X)$：事件X发生的不确定性。$P(X)$越小，$H(X)$越小，$P(X)$越大，$H(X)$越大。
  信息量的大小和它的不确定性有直接的关系，要搞清楚意见非常不确定的事情，就需要大量的信息。
  香农布朗就用比特（bit）来衡量信息量的多少
  $$ H(X)=-\sum_{i} p_i \log_{2}p_i$$
  熵的计算公式
  熵：表征一个物体内部的混乱程度。
  $$Entropy=-\sum_{i=1}^n p_i \ln_{p_i}$$
  Gini系数：$$Gini(p)=\sum_{k=1}^K p_k(1-p_k)=1-\sum_{k=1}^K p_k^2$$
  决策树划分节点的规则：节点熵迅速降低。熵降低的速度越快越好。将熵值最大的当做根节点，分类后，再继续判断下一层的熵值。

  KL散度-相对熵

  Kullback-Leibler(KL)divergence
  $$D_{KL}(P||Q)=\Bbb{E}_{x~P}[\log \frac{P(x)}{Q(x)}]$$
  KL散度性质：
• 非负性：KL散度为0当且仅当P和Q同分布。
• 非对称性：$D_{KL}(P||Q)\neq D_{KL}(Q||P)=$

交叉熵

cross-entropy
$$H(P,Q)=H(P)+D_{KL}(P||Q)$$

归纳算法

ID3

度量方法：信息获取量（information Gain）纯度差，也称为信息增益。例如通过A作为节点分类获取了多少信息 ：
$$Gain(D,a)=Ent(D)-\sum_{v=1}^V \frac{|D^v|}{D}Ent(D^v)$$
Ent(D)代表不纯度

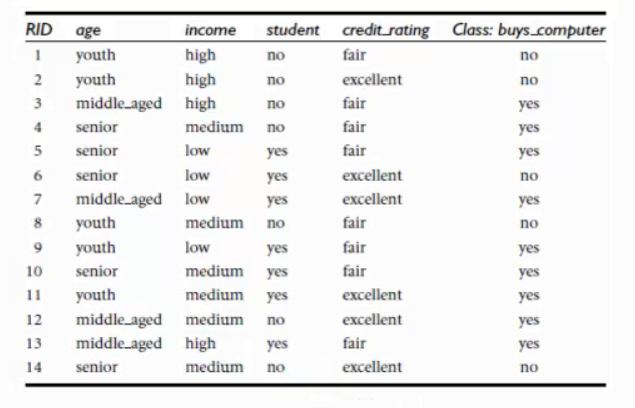
例如按照年龄区分时，得到信息获取量：

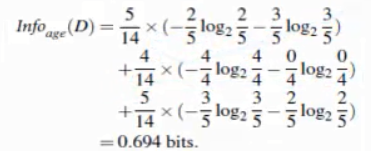
然后按照收入、是否是学生、信用率求得对应的值，用信息量最大的参数当做当前节点划分的依据。不断重复这个步骤，直到满足停止条件停止。

这个就是ID3算法的大致步骤。

C4.5

度量方法：Gain Ration
现在有一个极端的例子，给每个样本进行编号，然后按照编号弄一个决策树可不可以呢？答案当然是不可以。因为每个编号都是一类，这样无疑是最准确的，但是有一个问题就是泛化能力远远不够啊。这样做了是毫无意义的。由于ID3对于信息中类似索引的数值特别的敏感，这个属性会将决策树过分的划分出很多分支，造成模型效果性能较差。
C4.5是ID3算法的拓展，引入了增益率，比上自身的熵值。 因此我们用增益率来防止这个事情的发生。
$$Gain-ratio(D,a)=\frac{Gain(D,a)}{IV(a)}其中IV(a)=-\sum_{v=1}^V \frac{|D^v|}{|D|}\log_{2}\frac{|D^v|}{|D|}$$
属性A的可能取值数目越多，则IV(A)的值通常会较大。增益率会对取值数目较少的属性有所偏好，C4.5算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。

CART

Classification and Regression Trees
度量方法：Gini系数
$$Gain-index(D,a)=\sum_{v=1}^V \frac{|D^v|}{|D|}Gini(D^v)$$

评价函数

评价函数是评估所有叶子节点的纯度很大，所以定义评价函数C(T)。
$$C(T)=\sum_{t∈leaf}N_t·H(t)$$
$N_t$表示叶子结点的个数（相当于权重值），乘上熵值。评价决策树的优劣，C(T)的值越小越好。

停止条件

决策树的构建过程是一个递归的过程，所以需要确定停止条件，否则过程将不会结束。

• 一般一种最直观的方式是当每个子节点只有一种类型的记录时停止，但是这样往往会使得树的节点过多，导致过拟合问题（Overfitting）。
• 另一种可行的方法是当前节点中的记录数低于一个最小的阀值，那么就停止分割，将max(P(i))对应的分类作为当前叶节点的分类。

优化方案

策树高度过高，会导致模型的过拟合。这样如果存在错误样本，会导致模型性能下降。一般通过预剪枝、后剪枝优化决策树。

• 预剪枝：首先设定决策树最大深度，在决预剪枝在构建过程中，如果查过了最大深度则提前停止。
• 后剪枝：当构建完成决策树后，根据评价函数$$C_{\alpha}(T)=C(T)+\alpha|T_{leaf}|$$不光看$C(T)$损失函数，还要看叶子结点的个数越多，也要进行剪枝。$\alpha$是可以指定的。
  参数α≥0控制两者之间的影响，较大的α促使选择较简单的模型，较小的α促使选择较复杂的模型。剪枝就是当α确定时，选择损失函数最小的模型，子树越大，往往与训练数据的拟合越好，但是模型的复杂度就越高；相反，子树越小，模型的复杂度就越低，但是往往与训练数据的拟合不好，损失函数正好表示了对两者的平衡。

连续与缺失值

连续值处理
由于连续属性的可取值数目不再有限，因此不能直接根据连续属性的可取值来对接点进行划分，此时，连续属性离散化技术可派上用场，最简单的策略是采用二分法对连续属性进行处理。给定样本集D和连续属性A，假定A在D上出现了n个不同的取值，将这些值从小到大进行排序，记为${a_1,a_2…a_n}$，对相邻属性取值来说，在区间$(a_i,a_{i+1})$中取任意值所产生的划分结果相同，因此对连续属性A，可以考察包含n-1个元素的候选划分点集合。

需要注意，与离散属性不同，划分节点时，若当前节点划分属性为连续属性，该属性还可以作为其后代节点的划分属性。

缺失值处理
有时候会遇到不完整样本，某些属性值缺失，如果简单放弃不完整样本，显然是对数据的浪费。使用则需要解决两个问题：(1) 如何在属性值缺失的情况下进行划分属性选择？(2) 给定划分属性，若样本在该属性上的值缺失，如何对样本进行划分？
对问题一：令$\tilde{D}$表示在a上没有缺失值的样本子集。假定a有V个可能取值。 $\tilde{D}^v$表示a取$a^v$的样本子集。假定每个样本x赋予一个权重$w_x$，并定义:
$$\rho=\frac{\sum_{x∈\tilde{D}}w_x}{\sum_{x∈D}w_x}$$

$$\tilde{p_k}=\frac{\sum_{x∈\tilde{D}_k}w_x}{\sum_{x∈\tilde{D}}w_x}(1≤k≤|\upsilon|)$$

$$\tilde{r_v}=\frac{\sum_{x∈\tilde{D}^v}w_x}{\sum_{x∈\tilde{D}}w_x} (1≤v≤V)$$
a、ρ表示无缺失样本值所占比例。 表示第k类所占比例，$\tilde{r_v}$表示无缺失样本在属性a上取值$a^v$所占比例。固将增益计算式推广为：
$$Gain(D,a)=\rho \times Gain(\tilde{D},a)=\rho*\Bigl(Ent(\tilde{D})-\sum_{v=1}^V \tilde{r_v}Ent(\tilde{D^v})\Bigr)$$

对问题二：简单说就是让没有取值的x划入所有子节点，属性值调整为$\tilde{r_v}·w_x$

随机森林

决策树由于容易产生过拟合，出现了随机森林，减小了过拟合现象。
随机森林是通过多个决策树进行组合生成的。

python实现

数据是这样的，根据年龄、收入、是否是学生、信用数据构建决策树：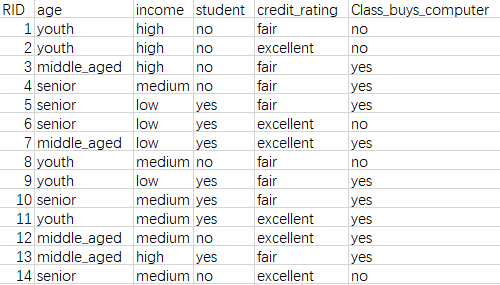

from sklearn.feature_extraction import DictVectorizer
import csv
from sklearn import preprocessing,tree
from sklearn.externals.six import StringIO
import pandas as pd
pd_data = pd.read_csv('data/tree.csv')
labelList=[]
featureList=[]
f= open('data/tree.csv','r',encoding='utf8')
reader = csv.reader(f)
labelList=[]
featureList=[]
for row in reader:
    labelList.append(row[len(row)-1])
    rowDict={}
    for i in range(1,len(row)-1):
        rowDict[pd_data.columns[i]]=row[i]
    featureList.append(rowDict)
featureList.pop(0)
labelList.pop(0)
vec=DictVectorizer()
dummyX=vec.fit_transform(featureList).toarray()
lb=preprocessing.LabelBinarizer()
dummyY=lb.fit_transform(labelList)
clf=tree.DecisionTreeClassifier(criterion='entropy')  # 默认为CART
clf=clf.fit(dummyX,dummyY)
with open('data/tree.dot','w') as f:
    f=tree.export_graphviz(clf,feature_names=vec.get_feature_names(),out_file=f)

windows中，可以安装Graphviz将dot文件转为pdf，可视化决策树。

dot -Tpdf tree.dot -o tree.pdf

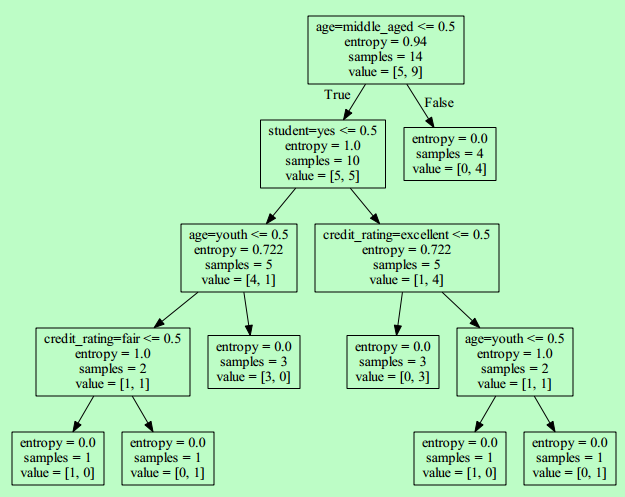
样本数据进行交叉验证：

from sklearn.cross_validation import train_test_split

(training_inputs,
 testing_inputs,
 training_classes,
 testing_classes) = train_test_split(dummyX, dummyY, train_size=0.75, random_state=1)
 clf=tree.DecisionTreeClassifier(criterion='entropy')  # 默认为CART，设置为ID3
clf=clf.fit(training_inputs,training_classes)
clf.score(testing_inputs, testing_classes)

可以看出，这个决策树的得分是0.5，是个很低的预测结果，原因可能是数据太少了，交叉验证后供决策树提供训练的数据不足。可以调整参数，尝试使用Gini系数得分也一样。

from sklearn.ensemble import RandomForestRegressor 
rf=RandomForestRegressor()  
rf.fit(training_inputs,training_classes)
rf.score(testing_inputs, testing_classes)

随机森林由于随机性，每次得出的结果不一定相同。