聚类算法

2018-04-24

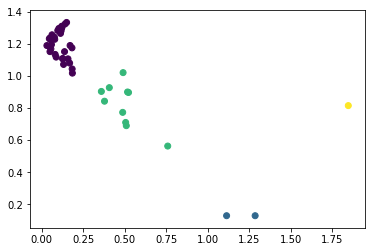
聚类可以说是一种无监督的学习，也就是说在训练样本中对应的标记信息是没有的，目标是通过对无标记训练样本的学习来揭示数据内在性质和规律，为进一步的数据分析提供基础。

聚类的任务

聚类试图将数据集中的样本划分为若干个通常是不相交的子集，每个子集称为一个“簇”。

性能度量

簇内相似度高，簇间相似度低。

外部指标：是将聚类结果与某个“参考模型”进行比较
内部指标：直接考察聚类结果而不利用任何参考模型。

距离计算

距离度量满足的基本性质：非负性、同一性、对称性、直递性

闵可夫斯基距离：$distmk=(n∑u=1|xiu−xju|p)1p$
- 如果p=2时，则表示欧氏距离
- 如果p=1时，则表示曼哈顿距离
有序属性：
无序属性：闵可夫斯基可以用于无序属性。对于无序属性可以采用VDM

原型聚类

原型聚类亦称“基于原型的聚类”，常用的原型聚类算法如下

K均值聚类(Kmeans)
学习向量量化
高斯混合聚类(GMM)

K值的确定：
知乎的回答

数据的先验知识，或者数据进行简单分析能得到
基于变化的算法：即定义一个函数，随着K的改变，认为在正确的K时会产生极值。如Gap Statistic（Estimating the number of clusters in a data set via the gap statistic, Tibshirani, Walther, and Hastie 2001），Jump Statistic （finding the number of clusters in a data set, Sugar and James 2003）
基于结构的算法：即比较类内距离、类间距离以确定K。这个也是最常用的办法，如使用平均轮廓系数，越趋近1聚类效果越好；如计算类内距离/类间距离，值越小越好；等。
基于一致性矩阵的算法：即认为在正确的K时，不同次聚类的结果会更加相似，以此确定K。基于层次聚类：即基于合并或分裂的思想，在一定情况下停止从而获得K。
基于采样的算法：即对样本采样，分别做聚类；根据这些结果的相似性确定K。如，将样本分为训练与测试样本；对训练样本训练分类器，用于预测测试样本类别，并与聚类的类别比较。

密度聚类

基于密度的聚类算法主要的目标是寻找被低密度区域分离的高密度区域。与基于距离的聚类算法不同的是，基于距离的聚类算法的聚类结果是球状的簇，而基于密度的聚类算法可以发现任意形状的聚类，这对于带有噪音点的数据起着重要的作用。

层次聚类

层次聚类也叫连通聚类方法，有两个基本方法：自顶而下和自底而上。自顶而将所有样本看做是同一簇，然后进行分裂。自底而上将初所有样本看做不同的簇，然后进行凝聚。这种聚类的中心思想是：离观测点较近的点相比离观测点较远的点更可能是一类。
过程如下：

把每个样本归为一类，计算两个类之间的距离；
寻找各类之间最近的两个类归为一类；
重新计算新生成的这个类与旧类之间的相似度；
重复2到3，直到所有样本归为一类停止。

实际上聚类过程就是建立了一棵树：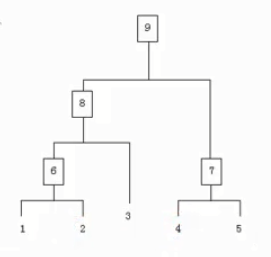
upload successful
可以在中间过程设置阈值，当两个类距离大于阈值，则迭代终止。

第三步相似度的度量有很多方法，例如：

两个类之间距离最近的两个样本的距离
两个类之间距离最远的两个样本的距离
两个类的样本平均距离
两个类的样本中位数的距离

神经网络

ART网络

ART（Adaptive Resonance Theory，自适应谐振理论）竞争学习的代表，是一种常用的无监督学习策略。该策略网络输出神经元相互竞争，每一时刻仅有一个竞争获胜的神经元被激活。其他神经元被抑制。包含比较层、识别层、识别阈值和重置模块。

SOM网络

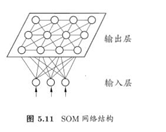
upload successful
SOM（Self-Organizing Map，自组织映射）网络是最常用的聚类方法之一：

竞争型的无监督神经网络
将高维数据映射到低维空间，并保持输入数据在高维空间的拓扑结构。即将高维空间中相似的样本点映射到网络输出层中邻近神经元
每个神经元拥有一个权向量
目标：为每个输出层神经元找到合适的权向量以保持拓扑结构

训练

网络接收输入样本后，将会确定输出层的“获胜”神经元（“胜者通吃”）
获胜神经元的权向量将向当前输入样本移动

import numpy as np
def kmeans(x,k,maxIt):
    numPoints,numDim=x.shape
    dataSet=np.zeros((numPoints,numDim+1))
    dataSet[:,:-1]=x
    centroids=dataSet[np.random.randint(numPoints,size=k),:]
#     centroids=dataSet[0:2,:]
    centroids[:,-1]=range(1,k+1)
    iterations=0
    oldCentroids=None
    while not shouldstop(oldCentroids,centroids,iterations,maxIt):
        print(iterations,dataSet,centroids)
        oldCentroids=np.copy(centroids)
        iterations+=1
        updateLabels(dataSet,centroids)
        centroids=getCentroids(dataSet,k)
    return dataSet
def shouldstop(oldCentroids,centroids,iterations,maxIt):
    if iterations>maxIt:
        return True
    return np.array_equal(oldCentroids,centroids)
def updateLabels(dataSet,centroids):
    numPoints,numDim=dataSet.shape
    for i in range(0,numPoints):
        dataSet[i,-1]=getLabelFromClosestCentroid(dataSet[i,:-1],centroids)        
def getLabelFromClosestCentroid(dataSetRow,centroids):
    label=centroids[0,-1]
    minDist=np.linalg.norm(dataSetRow-centroids[0,:-1])
    for i in range(1,centroids.shape[0]):
        dist=np.linalg.norm(dataSetRow-centroids[i,:-1])
        if dist<minDist:
            minDist=dist
            label=centroids[i,-1]
    print(minDist)
    return label        
def getCentroids(dataSet,k):
    result=np.zeros((k,dataSet.shape[1]))
    
    for i in range(1,k+1):
        oneCluster=dataSet[dataSet[:,-1]==i,:-1]
        result[i-1,:-1]=np.mean(oneCluster,axis=0)
        result[i-1,-1]=i
    return result        
x1=np.array([1,1])
x2=np.array([2,1])
x3=np.array([4,3])
x4=np.array([5,4])
testX=np.vstack((x1,x2,x3,x4))

result=kmeans(testX,2,10)
print(result)

层次聚类的实现

import numpy as np
from numpy import *
import os
from PIL import Image,ImageDraw
class Cluster_node:
    def __init__(self,vec,left=None,right=None,distance=0.0,id=None,count=1):
        self.vec=vec
        self.left=left
        self.right=right
        self.distance=distance
        self.id=id
        self.count=count
def L2dist(v1,v2):
    return np.linalg.norm(v1-v2,ord=2)
def hcluster(features,distance=L2dist):
    distances={}
    currentclustid=-1
    clust=[Cluster_node(array(features[i]),id=i) for i in range(len(features))]
    while len(clust)>1:
        lowestpair=(0,1)
        closest=distance(clust[0].vec,clust[1].vec)
        for i in range(len(clust)):
            for j in range(i+1,len(clust)):
                if (clust[i].id,clust[j].id) not in distances:
                    distances[(clust[i].id,clust[j].id)]=distance(clust[i].vec,clust[j].vec)
                d=distances[(clust[i].id,clust[j].id)]
                if d<closest:
                    closest=d
                    lowestpair=(i,j)
        mergevec=[(clust[lowestpair[0]].vec[i]+clust[lowestpair[1]].vec[i])/2 for i in range(len(clust[0].vec))]
        newcluster=Cluster_node(array(mergevec),left=clust[lowestpair[0]],right=clust[lowestpair[1]],distance=closest,id=currentclustid)
        currentclustid-=1
        del clust[lowestpair[1]]
        del clust[lowestpair[0]]
        clust.append(newcluster)
    return clust[0]

def extract_clusters(clust,dist):
    clusters={}
    if clust.distance<dist:
        return [clust]
    else:
        cl=[]
        cr=[]
        if clust.left!=None:
            c1=extract_clusters(clust.left,dist=dist)
        if clust.right!=None:
            cr=extract_clusters(clust.right,dist=dist)
        return cl+cr
def get_cluster_elements(clust):
    if clust.id>=0:
        return [clust.id]
    else:
        cl=[]
        cr=[]
        if clust.left!=None:
            c1=get_cluster_elements(clust.left)
        if clust.right!=None:
            cr=get_cluster_elements(clust.right)
        return cl+cr
def printclust(clust,labels=None,n=0):
    for i in range(n):
        print(' ',end='')
    if clust.id<0:
        print('-',end='')
    else:
        if labels==None:
            print(clust.id,end='')
        else:
            print(labels[clust.id],end='')
    if clust.left!=None:
        printclust(clust.left,labels=labels,n=n+1)
    if clust.right!=None:
        printclust(clust.right,labels=labels,n=n+1)

def getheight(clust):
    if clust.left==None and clust.right==None:
        return 1
    return getheight(clust.left)+getheight(clust.right)

def getdepth(clust):
    if clust.left==None and clust.right==None:
        return 0
    return max(getheight(clust.left),getheight(clust.right))+clust.distance

下面是几个城市的GDP等信息，根据这些信息，写一个SOM网络，使之对下面城市进行聚类。并且，将结果画在一个二维平面上。

//表1中，X。为人均GDP(元)；X2为工业总产值(亿元)；X。为社会消费品零售总额(亿元)；x。为批发零售贸易总额(亿元)；x。为地区货运总量(万吨)，表1中数据来自2002年城市统计年鉴。

//城市 X1 X2 X3 Xa X5
北京 27527 2738.30 1494.83 3055.63 30500
青岛 29682 1212.02 182.80 598.06 29068
天津 22073 2663.56 782.33 1465.65 28151
烟台 21017 298.73 92.71 227.39 8178
石家庄 25584 467.42 156.02 763.46 12415
郑州 17330 261.80 215.63 402.98 7373
唐山 19387 338.67 95.73 199.69 14522
武汉 17882 1020.84 685.82 1452 16244
太原 13919 304.13 141.94 155.22 15170
长沙 26327 241.76 269.93 369.83 7550
呼和浩特 13738 82.23 69.27 108.12 2415
衡阳 12386 61.53 63.95 72.65 3004
沈阳 21736 729.04 590.26 1752.4 15156
广州 42828 2446.97 1166.10 3214.19 24500
大连 34659 1003.56 431.83 728.08 19736
深圳 152099 3079.63 609.26 801.06 5167
长春 24799 900.26 309.75 173.99 10346
油头 19414 192.93 112.96 280.84 1443
哈尔滨 20737 402.73 360.38 762.94 8814
湛江 15290 228.45 99.08 149.16 5524
上海 40788 6935.57 1531.89 3921.2 49499
南宁 17715 109.39 142.08 264.32 3371
南京 26697 1579.21 401.20 1253.73 14120
柳州 17598 256.76 68.93 159.44 3397
徐州 19727 295.73 108.17 187.39 7124
海口 24782 100.13 81.03 142.54 2018
连云港 17869 112.18 47.94 134.89 4096
成都 22956 412.23 400.56 754.07 23724
杭州 31784 1615.63 373.28 1788.29 15841
重庆 9778 870.82 389.60 823.72 29470
宁波 46471 751.58 167.70 529.68 11182
贵阳 13176 207.95 108.93 285.27 4885
温州 29781 381.93 233.44 272.84 6292
昆明 24554 303.78 227.44 428.64 12084
合肥 19770 330.14 140.14 328.98 2903
西安 16002 449.14 323.37 558.27 7728
福州 33570 379.51 209.72 613.24 7280
兰州 16629 354.30 163.97 374.9 5401
厦门 42039 803.29 186.55 620.47 2547
西宁 7261 38.00 48.95 91.14 1837
南昌 19923 238.82 14.09 348.21 3246
银川 12779 77.74 41.22 53.16 1573
济南 25642 616.97 323.08 462.39 13057
乌鲁木齐 19793 251.19 129.05 277.8 9283

import pandas as pd
result = pd.read_csv('./data/diqu.csv',sep='\s+',encoding='gbk')
# 将result归一化
# 标准化操作：from sklearn.preprocessing import StanderdScaler
# result_std=StandardScaler().fit_transform(reslut)
result_norm = (result.iloc[:,1:] - result.iloc[:,1:].min()) / (result.iloc[:,1:].max() - result.iloc[:,1:].min())
result_norm.head()
from sklearn.cluster import KMeans
kmeans_model=KMeans(n_clusters=4,random_state=1)
senator_distances=kmeans_model.fit_transform(result_norm.iloc[:,1:])
labels=kmeans_model.labels_
print(pd.crosstab(labels,result['城市']))
# democratic_outliers=votes[(labels==1)&(result['party']!='D')]
import matplotlib.pyplot as plt
plt.scatter(x=senator_distances[:,0],y=senator_distances[:,1],c=labels)
plt.show()

upload successful