基本概念
- 条件概率的概念:A和B是两个事件,事件A发生的条件下,事件B发生的概率,表示为:$P(A|B)=P(AB)/P(B)$。
事件独立:$P(AB)=P(A)P(B)$。
求和$P(A+B)=P(A)+P(B)-P(AB)$。
求差$P(A-B)=P(A)-P(AB)$。
乘积:$P(AB)=P(A)P(B|A)=P(B)P(A|B)$。
联合分布:$\sum_{A} P(A,B)=P(B)$
$P(B)=\sum_{B|A}P(A)$
联合分布条件概率:$P(S|W)=\frac {P(S,W)}{P(W)}$
$P(A,B|C)=P(A|B,C)P(B|C)$ - 贝叶斯公式:
$P(B│A)=\frac{P(B)P(A|B)}{P(A)}$。
由全概率公式,当$B1、B2、B3……∈B,A⊂∑B_i$时,$P(B_i│A)=P(B_i)P(A|B_i)/(∑P(B_j)P(A|B_j))$。- $P(B_i)$先验概率
- $P(B_i│A)$为后验概率。
贝叶斯分类器是利用概率的知识完成数据的分类任务,在机器学习中使用贝叶斯决策论实施决策的基本方法也是在概率的框架下进行的,它是考虑如何基于这些概率和误判损失来选择最优的类别标记。
贝叶斯决策论
假设有N种可能的类别标记$y=(c_1,c_2….c_N)$,$λ_{ij}$是将一个真实标记为$c_j$的样本误分类为$c_i$所产生的损失。基于后验概率$P(c_i|x)$可获得奖样本x分类为$c_i$所产生的期望损失,即在样本x上的“条件风险”。
$$R(c_i|x=\sum_{j=1}^Nλ_{ij}P(c_j|x))$$
机器学习的过程就是要寻找一个判定准则:$h:x–>y$以最小化总体风险。
为最小化总体风险,只需要在每个样本上选择哪个能使条件分析最小的类别标记。
$$h^(x)=arg min R(c|x)$$
此时,$h^$称为贝叶斯最优分类器,与之对应的总体风险$R(h^)$称为贝叶斯风险。则$1-R(h^)$反映了分类器所能达到的最好性能。
- 生成式模型: 先对联合概率分布P(x,c)建模,然后由此获得P(c|x),如:贝叶斯分类器。
- 判别式模型: 给定x,通过直接建模P(c|x),预测c。如:决策树、BP神经网络、支持向量机
极大拟然估计
概率模型的训练过程就是参数估计过程,采用极大拟然估计就是试图在所有的可能的取值中,找到一个能使数据出现的“可能性”的最大值。
- 频率主义学派(Frequentist):参数虽然未知,但是客观存在固定值,所以可以通过优化似然函数等准则确定参数值。极大似然估计(Maximum Likelihood Estimation,MLE)是根据数据采样来估计概率分布的。
- 贝叶斯学派(Bayesian):参数是未观察到的随机变量,其本身也可有分布,因此,可假定参数服从一个先验分布,然后基于观测到的数据来计算参数的后验分布。
朴素贝叶斯分类器
朴素贝叶斯分类器(Naïve Bayes classifier):基于贝叶斯公式来估计后验概率 的主要困难在于求类条件概率 是所有属性上的联合概率,难以从有限的训练样本直接估计得到。为了解决这个问题,提出朴素贝叶斯分类器 它采用了“属性条件独立假设”对已知类别,假设所有属性相互独立,换言之,假设每个属性独立地对分类结果发生影响。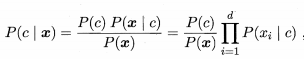
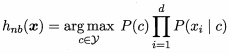
半朴素贝叶斯分类器
为了降低贝叶斯公式中估计后验概率$P(c|x)$的困难,提出使用朴素贝叶斯分类器采用属性条件独立性假设,然而在现实任务中这个假设很难成立,因此就提出半朴素贝叶斯分类器(Sem-naïve Bayes classifiers),它的基本思想是适当考虑一部分属性间的相互依赖信息,从而既不需要完全联合概率计算,又不至于彻底忽略了比较强的属性依赖关系。
独依赖估计(One-Dependent Estimator,ODE)每个属性在类别之外最多仅依赖于一个其他属性。最直接的做法,假设所有属性都依赖于同一属性,称为为超父(super-parent ODE)。TAN(Tree Augmented naïve Bayes)使用最大生成树算法,将属性间依赖关系生成最大带权生成树,保留了强相关属性之间的依赖性。AODE(Average的 One-Dependent Estimator)基于集成学习机制,尝试将每个属性作为超父来构建SPODE,最终返回具有足够支撑的SPODE集成作为最终结果。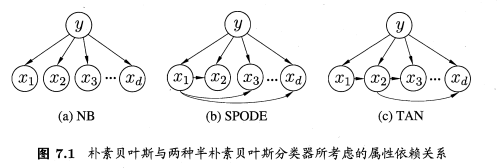
贝叶斯网
贝叶斯网是借助有向无环图(DAG)来刻画属性之间的依赖关系,并使用条件概率表(CPT)来描述属性的联合概率分布
结构
学习
推断
经典贝叶斯问题
A女士怀疑自己得了某种肝炎,希望在医院做一次检测。医生告诉A女士,她所属的人群得此种肝炎的概率仅有千分之一。但A女士不放心,还是坚持做了测试。然而很不幸,测试结果为阳性。现在已知测试仪器的正确率为95%,那么A女士确实得了肝炎而非误诊的概率为多少?
