神经元（neuron）模型
神经网络是由具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。
神经网络中最基本的成分是神经元（neuron）模型，即“简单单元”，在生物神经网络中，每个神经元与其他神经元相连，当它“兴奋”时，就会向相连的神经元发送化学物质，从而改变这些神经元内的电位；如果某神经元的电位超过一个“阈值（threshold）”，那么它就会被激活，即“兴奋” 起来，向其他神经元发送化学物质。
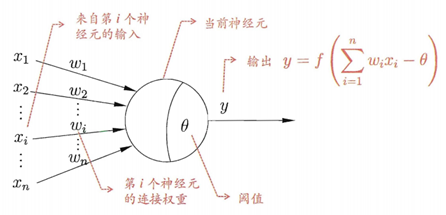
激活函数
理想激活函数是阶跃函数，0 表示抑制神经元而1表示激活神经元
阶跃函数具有不连续、不光滑等不好的性质，常用的是Sigmoid函数
Sigmoid函数
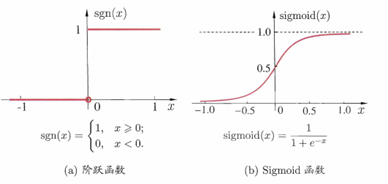
Sigmoid函数可能在较大范围内变化的输入值挤压到（0,1）输出值范围内，因此有时也称为”挤压函数”
把这样许多个神经元按一定的层次结构连接起来，就得到了神经网络。
ReLu函数
tanh
softmax
$max(0,(y-\widehat{y}))$
损失函数
- 回归问题：SSE（Sum of Squared Error）均方误差和
- 分类问题：CE（Cross Entropy）交叉熵
感知机（Perceptron）与多层网络
感知机有两层神经元组成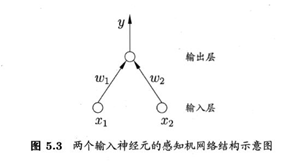
权重 及阈值θ通过学习获得，阈值θ可看做一个固定输入为-1的哑结点（dummy node）所对应的权重 。这样权重和阈值可以统一学习。对训练样例(x,y)，感知机输出 ，学习规则：
$$w_i←w_i+\nabla{w_i}$$
$$\nabla{w_i}=η(y-\widehat{y})x_i$$
η∈(0,1)称为学习率(learning rate)。
感知机只有输出层神经元进行激活函数处理，即只拥有一层功能神经元。与或非问题都是线性可分（linearly separable）。感知机对线性可分学习过程一定收敛，非线性可分问题w难以稳定下来，不能求合适的解，如下图D。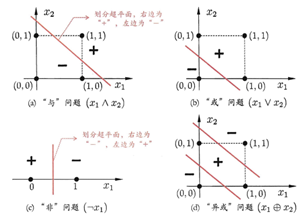
要解决非线性可分问题，需要考虑使用多层功能神经元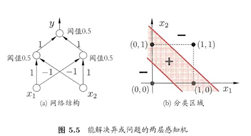
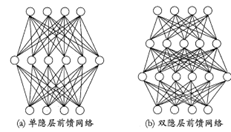
网络结构中，输入层与输出层之间的神经元层成为隐含层（hidden layer），每层神经元与下一层神经元完全互联，神经元之间不存在同层连接，也不存在跨层连接，称为多层前馈网络结构(multi-layer feedforward nerual networks)
- 多层网络：包含隐层的网络
- 前馈网络：神经元之间不存在同层连接也不存在跨层连接
隐层和输出层具有激活函数，所以这两层的神经元亦称“功能单元”。多层前馈网络有强大的表示能力。只需一个包含足够多神经元的隐层，多层前馈神经网络就能以任意精度逼近任意复杂度的连续函数。设置隐层神经元数，通常用“试错法”。
- 主要特点：信号是前向传播的，而误差是反向传播的。
- 主要过程：信号的前向传播，从输入层经过隐含层，最后到达输出层
- 误差的反向传播，从输出层到隐含层，最后到输入层，依次调节隐含层到输出层的权重和偏置，输入层到隐含层的权重和偏置
误差逆传播算法——BP神经网络
误差逆传播（error BackPropagation，简称BP）它是迄今为止最成功的神经网络学习算法，现实任务中使用神经网络时，大多在使用BP算法进行训练多层前馈神经网络，还可用于训练例如递归神经网络。
链式法则
$y=g(x)$，$z=h(y)$，$$\nabla{x}→\nabla{y}→\nabla{z} , \frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}$$
$x=g(s)$，$y=h(s)$，$z=k(x,y)$，$$\nabla{s}→\nabla{x},\nabla{y}→\nabla{z} , \frac{dz}{ds}=\frac{dz}{dx}\frac{dx}{ds}+\frac{dz}{dy}\frac{dy}{ds}$$
BP算法过程
给定训练集：$D=((x_1,y_1),(x_2,y_2)….(x_m,y_m)),x∈\Bbb{R}^d,y∈\Bbb{R}^l,$
输入：d维特征向量，（d个属性）；
输出：L个输出值（l维实值向量）；
隐层：假定使用q个隐层神经元；
输出层权重：$w_{ij}$；隐层权重：$v_{ij}$；输出层阈值：$θ_i$；隐层阈值：$γ_i$
隐层输入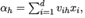
；
输出层输入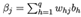
；
隐层第h个神经元输出：bh；
假定功能单元均使用Sigmoid函数 。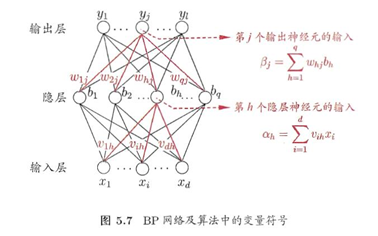
对训练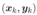
，假定输出为
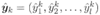，即
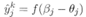，则网络在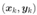
的均方误差为
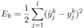，未知的参数包括隐层及输出层权值、阈值。
BP通过迭代学习，在每一轮采用广义的感知机学习规划对参数进行更新估计：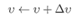
。BP算法基于梯度下降策略（gradient descent），以目标负梯度方向对参数进行调整。对于误差Ek，给定学习率：η：
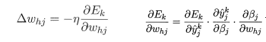
由于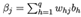
，可得到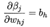
。
Sigmoid函数有以下性质：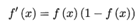
，所以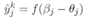
：
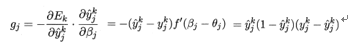
最终推得：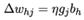
其他参数的推导式同样的方法：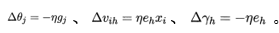
。
其中：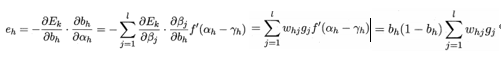
学习率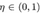
，控制迭代中的更新步长，太大容易震荡，太小则收敛过慢。其中wθ与vγ的学习率不一定相等。
BP算法流程
算法的工作流程：
标准BP算法与累计BP算法
主要目标：最小化训练集D上的累计误差 。前面算法更新规则是基于单个Ek推导的，也称作“标准BP算法”。若使用基于累计误差最小化的更新规则，成为累计误差逆传播算法（accumulated errror backpropagation）。两者都很常用：
| ————- |—–:|
|标准BP算法| 1、每次针对单个训练样例更新权值与阈值；2、参数更新频繁，不同样例可以抵消，需要多次迭代|
|累计BP算法| 1、其优化目标是最小化整个训练集上的累计误差；
2、读取整个训练集一遍才对参数进行更新，参数更新频率较低|
累计BP算法更新频率低，防止不同样例导致训练出现抵消的现象。在很多任务中，累计误差下降到一定程度后，进一步下降会非常缓慢，这是标准BP算法往往会获得较好的解，尤其当训练集非常大时效果更明显。
缓解过拟合
主要策略
- 早停early stopping
将训练数据分为训练集和验证集。训练集计算梯度和更新，验证估计误差。
1、若训练误差连续a轮的变化小于b,则停止训练
2、使用验证集：若训练误差降低，验证误差升高，则停止训练。
返回具有最小验证误差的链接权重和阈值。 - 正则化
regularization 在误差目标函数中，增加一项描述网络复杂度：例如连接权和阈值的平方和
误差目标函数改为： ， 用于对经验误差和网络复杂度进行折中。偏好比较小的连接权和阈值，使网络输出更“光滑”
全局最小与局部极小
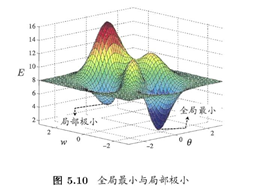
神经网络的训练过程可看作一个参数寻优过程：
在参数空间中，寻找一组最优参数使得误差最小
特点：存在多个“局部极小”；只有一个“全局最小”
常用策略跳出局部极小
- 不同参数进行初始化
- 模拟退火（simulated annealing） 以一定概率接收比当前解更差的结果，每部迭代中，接受次优解的概率随时间推移而降低。
- 随机梯度下降 计算梯度时增加随机因素，即使陷入局部极小也有机会跳出继续搜索。
- 遗传算法（genetic algorithms）
其他常见神经网络模型
RBF网络
RBF（Radial Basis Function，径向基函数）网络在分类任务中除BP之外最常用的一种
• 单隐层前馈神经网络
• 使用径向基函数作为隐层神经元激活函数ρ： ，定义为样本x到数据中心ci之间欧式距离的单调函数，常用高斯径向基函数。 。ci表示隐层神经元对应的中心、wi表示权重。
• 输出层是隐层神经元输出的线性组合
训练RBF网络：
• 确定神经元中心ci，常用的方式包括随机采样、聚类等
• 利用BP算法等确定参数wi和βi。
ART网络
ART（Adaptive Resonance Theory，自适应谐振理论）竞争学习的代表，是一种常用的无监督学习策略。该策略网络输出神经元相互竞争，每一时刻仅有一个竞争获胜的神经元被激活。其他神经元被抑制。包含比较层、识别层、识别阈值和重置模块。
SOM网络
SOM（Self-Organizing Map，自组织映射）网络是最常用的聚类方法之一：
• 竞争型的无监督神经网络
• 将高维数据映射到低维空间，并保持输入数据在高维空间的拓扑结构。即将高维空间中相似的样本点映射到网络输出层中邻近神经元
• 每个神经元拥有一个权向量
• 目标：为每个输出层神经元找到合适的权向量以保持拓扑结构
训练
• 网络接收输入样本后，将会确定输出层的“获胜”神经元（“胜者通吃”）
• 获胜神经元的权向量将向当前输入样本移动
级联相关网络：“构造性”神经网络的代表
构造性神经网络：将网络结构也当做学习的目标，并在训练过程中找到最符合的网络结构。是结构自适应网络的重要代表。
训练
• 开始时只有输入层和输出层
• 级联（Cascade）：新的隐层节点逐渐加入，从而创建起层级结构
• 相关（Correlation）：最大化新节点的输出与网络误差之间的相关性
Elman网络：递归神经网络的代表
• 网络可以有环形结构，可让使一些神经元的输出反馈回来最为输入
• t 时刻网络的输出状态： 由 t 时刻的输入状态和 t-1时刻的网络状态共同决定
Elman网络是最常用的递归神经网络之一
• 结构与前馈神经网络很相似，但隐层神经元的输出被反馈回来
• 使用推广的BP算法训练
Bolyzmann机：”基于能量的模型”的代表
深度学习
• 卷积神经网络CNN
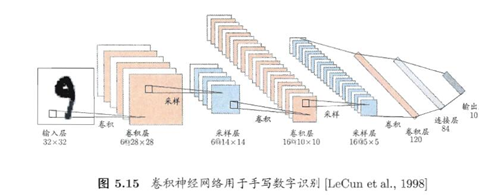
• 每个卷积层包含多个特征映射，每个特征映射是一个由多个神经元构成的“平面”，通过一种卷积滤波器提取输入的一种特征
• 采样层亦称“汇合层”，其作用是基于局部相关性原理进行亚采样，从而在减少数据量的同事保留有用信息
• 连接层就是传统神经网络对隐层与输出层的全连接
典型的深度学习模型就是很深层的神经网络